Boggle is a word game designed by Allan Turoff and originally distributed by Parker Brothers. The game is played using a plastic grid of lettered dice, in which players attempt to find words in sequences of adjacent letters… Wikipedia
Problem Statement
This problem is also said as Jigsaw Crossword Puzzle. You are given a board containing MxN cells, each letter containing an alphabet of the English language. The goal of the program is to traverse through different cells to find a given word such that the following conditions are satisfied.
-
The letters of the word must be formed by traveling through a series of adjacent cells. i.e, the next letter in the word can be in any of the eight cells surrounding it.
-
If there is a path drawn as the letters of the words are discovered, the path must not cross over itself.
-
The word should not use multiple instances of the same cell.
Result should be the number of times the given word occurs!
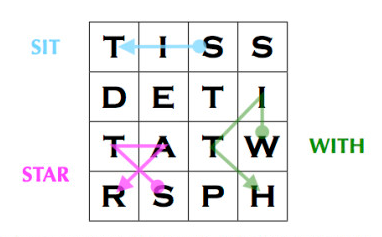
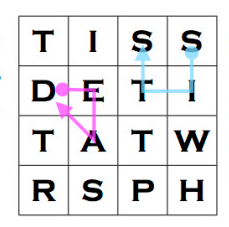
Paths made using pink are invalid
The Input:
findme - (the word to be found)
M - (the number of rows)
N - (the number of columns)
a b c d e … (n elements)
.
.
.
.(m rows)
z y s x o …
Input Format:
'word'
5 x 3
r a y x d
w e t r o
o r d o z
Output Format:
output : 1
DIY : It is highly recommended to try solving it without looking ahead!
Algorithm / Pseudo Code
This part describes the algorithm or pseudo code for boggle solver.
- Step 1: Take all required inputs
- Step 2: We know that we can move to 8 adjacent cells. So we will try to
generate a tree starting with every letter in the gridas root - Step 3: Add all adjacent letters as the child. Note that some cases can have less than eight child.
- Step 4: We should take care of the infinite loop. If we keep adding every element then the tree never terminates. We need a way to reduce our space with every addition. So that in a straight path the
characterat sameindexis not repeated. In technical term the above process is known asDFS. - Step 5: After every addition check if the word is found.
- Step 6: If the word is found check if that word has crossover(think on it)? If
nothen increment the value of your matches. - Step 7: After exhausting the search for all the node print out the result!
DIY : This should give you some hint! Follow these steps and try building the code you started!
Code
It is OK to fail. It is not OK to give up!
You tried and you found it difficult, it is find. I have also found problems difficult. What I do it try to solve them, if I cannot, I see how others have done it. Then I make sure that next time I can do it for sure!
I have commented out most of the portions of my code. I have also left it unoptimized for better readability. If you find any line difficult to grasp, feel free to comment below. Here is the code: